前言

上一篇我們以航空公司的每月乘客人數為例，使用 LSTM 模型預測下個月的乘客數，其中牽涉到『時間序列分析』(Time Series Analysis)一些重要的觀念，在現實環境中，還有一些場景會常碰到，應該如何處理，再補充一些資料，與大家分享：

1. 如何讓訓練資料達到穩態(stationarity)?
2. LSTM如何處理『多變量』(Multivariate)分析?
3. LSTM如何處理『多階段』(Multi-step)分析?

穩態(stationarity)

『穩態』以白話文來講，就是平均數與變異數不會因時間改變而有顯著差異，例如，下圖乘客人數隨著時間改變，人數有逐漸增多的趨勢，為了區隔『波動』與『趨勢』，我們會希望先消除『趨勢』，單獨預測『波動』，預測完後，再將資料還原回去。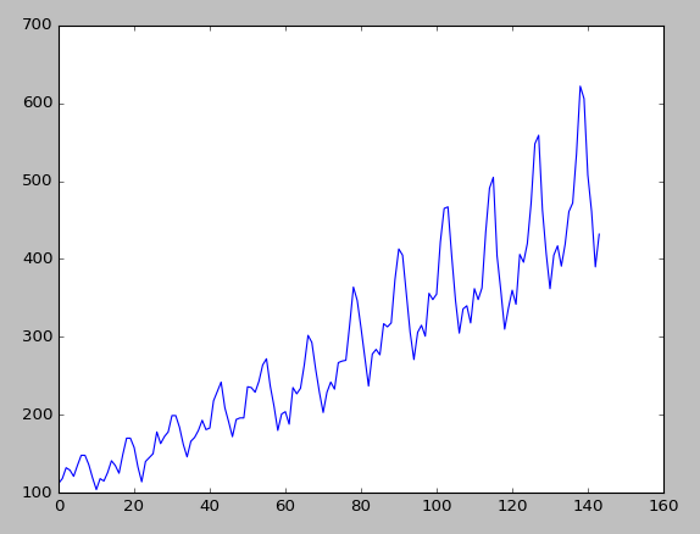

圖. 航空公司每月乘客人數

上次討論到 ARIMA 模型有三個參數p、q、d， 分別對應到自迴歸(Autoregressive，AR)期數、移動平均(Moving Average，MA)期數及差分階數，p、q 可以透過ACF及PACF觀察而得到適當的數值，d 則可以實際用差分函數(diff)轉換資料，繪製圖形觀察，波動是否達成穩態。通常，我們使用一階差分，即『當期資料 減 前一期資料』，就可以達到穩態，我們實際寫程式轉換航空公司每月乘客人數看看，如下圖：

import pandas
import matplotlib.pyplot as plt
dataset = pandas.read_csv('international-airline-passengers.csv', usecols=[1], engine='python', skipfooter=3)
# 一階差分
dataset1 = dataset.diff(1)
plt.plot(dataset1)
plt.show()

結果如下圖，『趨勢』去除了，但是變異數卻有擴大的趨勢，這就不是一個適合作時間序列分析的資料集，必須再將資料轉換，筆者找了scipy、Pandas、statsmodels的相關 de-trend 及log函數都無效，跟讀者抱歉，俟後找到答案，再與讀者分享。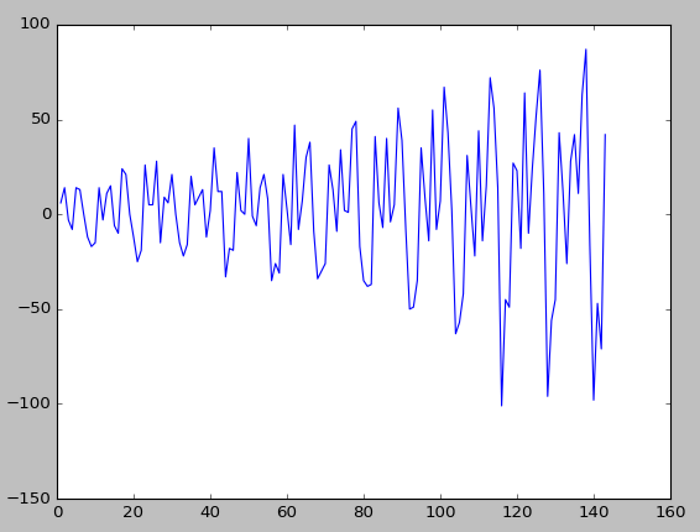

圖. 航空公司每月乘客人數資料，使用一階差分後的折線圖

我們再看一個實際案例，我下載1994~2013年台積電的每日股價資料，作一階差分，如下，第一個圖為原始資料，第二個圖為處理後的圖形，結果就非常理想，平均數與變異數都不因時間改變而有顯著差異：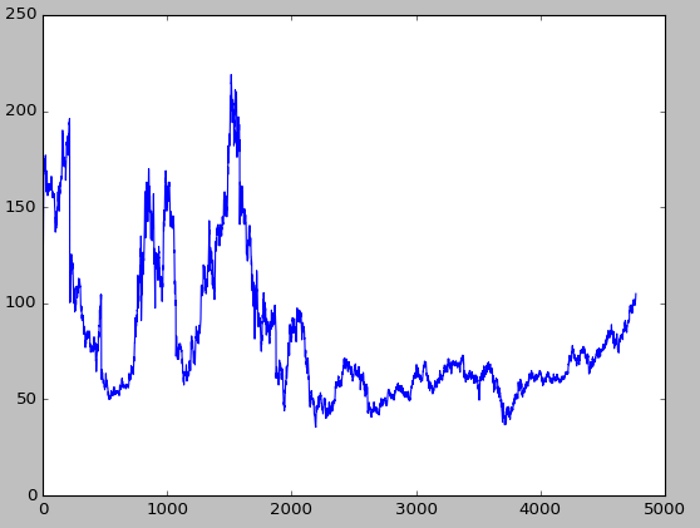

圖. 1994~2013年台積電的每日股價資料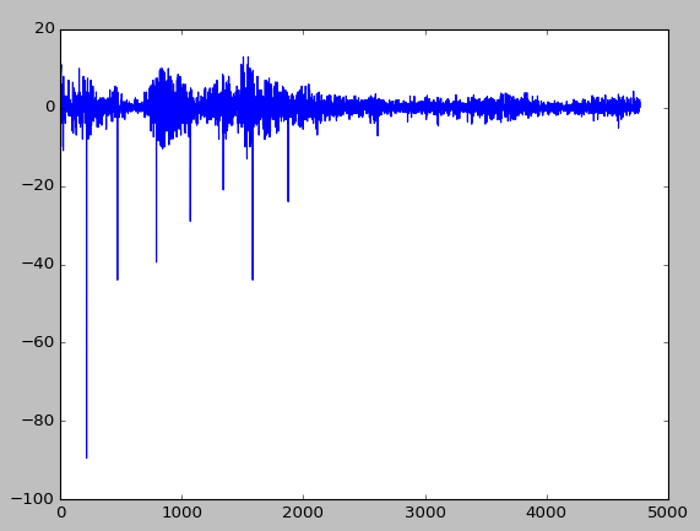

圖. 1994~2013年台積電的每日股價資料，使用一階差分後的折線圖

除了少數幾天股價，因急漲/急跌，變異較大，其他大致符合『平均數與變異數都不因時間改變而有顯著差異』的假設。

LSTM如何處理『多變量』(Multivariate)分析

我們之前的討論其實都是『單變量分析』(Univariate Analysis)，均以單一變數預測下一期的預估值，但實際的問題可能複雜的多，例如，台灣股市行情常受美、日、港的股市影響，又例如，股市也可能同受利率、匯率、通貨膨脹率、經濟成長率影響，而這些率又互相影響，這種模型研究就是『多變量分析』(Multivariate Analysis)，相對於 LSTM 要如何處理呢? 這個問題在『時間序列分析』處理非常複雜，但是，在LSTM處理就相對簡單多了。

在此舉一例說明，範例取自『Multivariate Time Series Forecasting with LSTMs in Keras』一文，該文主要是以北京的空氣品質監測資料集，探討多項監測變數對空氣污染的影響，原始資料格式如下：

圖. 空氣品質監測資料集的原始資料格式

圖. 空氣品質監測資料集的LSTM input資料格式

上一篇只有(X, Y)，多變量就變成(X1, X2, ..., X8)，因此，除了時間以外，我們又多了變數類別，因此，原來的input資料由2維變為3維，程式碼如下：

# reshape input to be 3D [samples, timesteps, features]
train_X = train_X.reshape((train_X.shape[0], 1, train_X.shape[1]))

模型不變，只要改變 input/output 資料的維度即可，比起『時間序列分析』要Arch/Garch一堆變形，簡單多了，至少不用讀完一本書，才可以動手作。

LSTM如何處理『多階段』(Multi-step)分析

上一篇我們只用前一期資料來預測下一期(當然前一期會受前前一期影響)，如果，我們希望改為以前三期作為input，預測下一期的銷售量，也就是所謂滾動式的預測(Rolling Forecast)，1/2/3月預測4月、2/3/4月預測5月、3/4/5月預測6月，以此類推，在『時間序列分析』ARIMA模型處理很簡單，只要將p改為3即可，但是，使用LSTM模型不要忘記，它有記憶的功能，所以，在每一輪預測時，記得要把記憶重置(reset_states)，程式碼如下：

# fit network
for i in range(nb_epoch):
    model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)
    model.reset_states()
return model

詳細說明可參閱『Multi-step Time Series Forecasting with Long Short-Term Memory Networks in Python』一文。

結語

特別整理這一篇的目的，在於提醒我們在面對問題時，須先了解模型的假設與原理，若違反模型假設(例如，時間序列分析的資料須呈穩態)或忽略其原理(例如，LSTM有記憶的功能)，則預測結果不是過度擬合，就是預測失準，這些都不會顯現在程式碼中，應該是很難除錯的。

相關的資料集及程式碼都可在原文中下載，由於，筆者並無任何貢獻，就不好意思收錄在自己的github中了。